As part of my PhD thesis, I developed a framework to formalize SAT solving. I still continue to expand it. The general organization is given by the following graph: 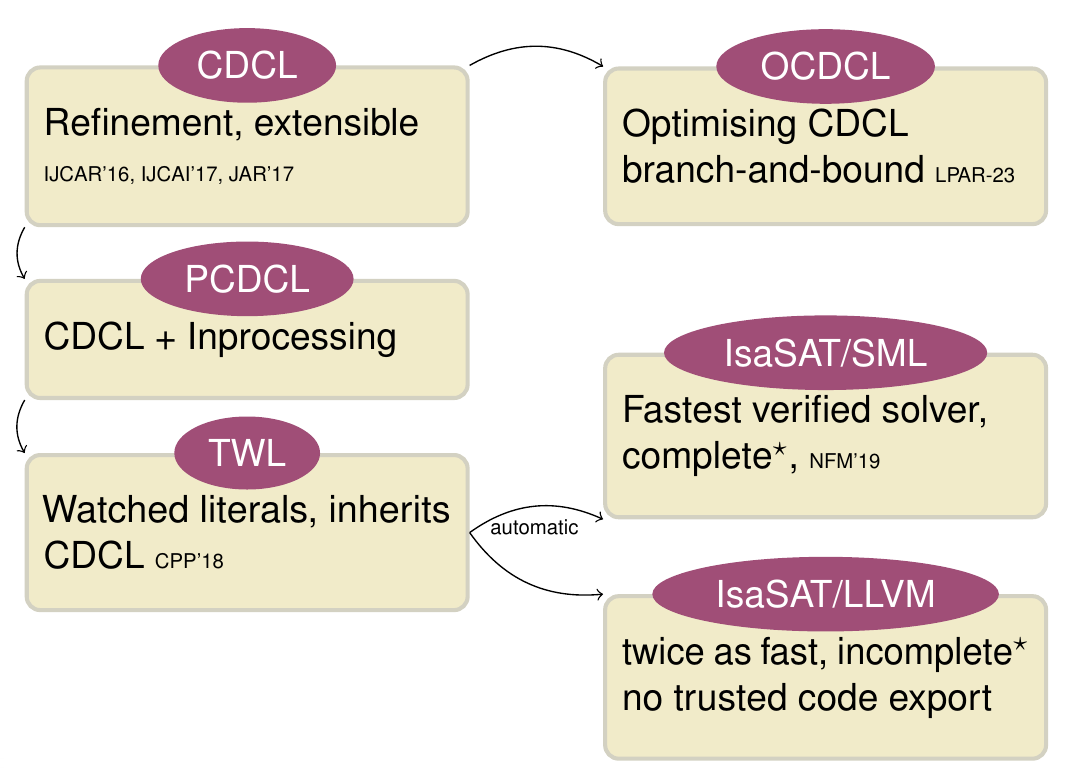. If you want to have a look at the sources, look at the IsaFoL repository (this is the latest bleeding age version, so it is sometimes broken) and the Isabelle-generated HTML documentation (look at the “IsaFoL” version at the bottom to know the corresponding git ID).

SAT Solver Framework

I start with an abstract specification of CDCL and prove termination and correctness. CDCL is specified as an abstract transition system. I have developped two variants: one based on Nieuwenhuis et al. and a more concrete one based on Weidenbach’s version of CDCL. I show that the latter version refines (specializes) the former.

Pragmatic CDCL

The PCDCL (standing for pragmatic CDCL) and IsaSAT/LLVM have not yet been described in a publications, but have already been included in the Isabelle formalization. It is currently used for very simple simplifications, namely removing true clauses and (unconditionally) false literals from clauses. This is very important to do (in particular because in some problems from the SAT Competition several thousands units are generated per minute), but this is already beyond the CDCL framework from my thesis.

Watched Literals

First I developed a transition that includes the watched listeral (with blocking clauses) optimization to efficiently find propagations and conflicts.

From there one, I enter the nondeterminism refinement monad. It is a way to write nondeterministic programs (like the transition systems), while still getting closer to programs (e.g., invariants and loops).

Heuristics and Executable Code

Now comes the level where the nondeterminstic operations are replaced by deterministic heuristics. This level is not so important from the Isabelle point-of-view, but is absolutely critical for performance. It is very easy to destroy performance by restarting too often (or not often enough).

Finally I use Peter Lammich’s Isabelle-LLVM to generate code in LLVM’s intermediate language. The code can be compiled with clang. Combined with a hand-written parser and printer of the output, the code can be fed with a DIMACS like any other SAT solver.

During my PhD thesis I used the (older) Refinement Framework to generate Standard ML. This allowed me to prove completeness (for a powerful-enough compiler and machine), but the code was twice as slow as the LLVM-generated version (same Isabelle code!) – and in the end the completeness guarantees were similar.

Correctness

In essence, the completeness mentioned in the graph above, means completeness unless you cannot allocate enough memory:

• In the Standard ML modelisation of Isabelle, arrays can be accessed by arbitrary sized integers. However, compilers do not have to support that. Therefore, in practice, the memory is limited to around 2⁶¹ bits (for MLton) to represent the clauses and their headers. Such machines currently do not exist (and filling so much memory takes a very long time too).
• In LLVM, we are restricted to a certain number of clauses (it must fit in a 64-bit integer!) and all clauses have fit in array (like in standard ML with the limit of 2⁶³ bits). With enough memory (more than 2⁶³ bits) and enough time, the answer could become “UNKNOWN” (but no overflow will lead to a wrong error!)